Based on a lecture given at the Art Gallery of NSW 19 September 2001
Revised 5 September 2007
Introduction
What, if anything, do mathematics and art have in common? Some people see these two disciplines as incompatible by definition. Others see mathematics within art, at least in areas such as geometry and perspective. However, it could be argued that this connection is no more significant than that between any discipline and the tools used by its practitioners. For example, no-one argues that electronics is within literature simply because many writers use electronic computers. On the other hand, some people look at complex geometric forms or shapes, declare them “beautiful” and infer from this that there is art within mathematics.
In this essay, however, I will attempt to dig a little deeper, to examine the principles and philosophies of these two disciplines and how they might relate.
Beauty and proportion
Since the time of the Ancient Greeks, and possibly earlier, artists have realised the central role played by proportion in the concept of beauty. And proportion, being a mathematical concept, lends itself to formal definitions.
So, let’s consider some basic aesthetic tasks that concern proportion.
The first task is to divide a line segment into two so that the two smaller pieces have a “pleasing” relationship to each other.
How could we do this? We could divide the segment into two equal parts (in a ratio of 1 : 1, or “one as to one”). A little too obvious? Too boring? What if we were to divide it so that one part were twice as long as the other (a ratio of 2:1 or 1:2)? Perhaps that would make the pieces too dissimilar in size. Perhaps we could divide it in the ratio of 2 : 3 or 3 : 2?
A task such as this, although seemingly very simple, is what confronts every landscape artist when considering where to place the horizon.
Is there an ideal answer? Probably not, given that we all have slightly different concepts of “pleasing” and “beautiful”. However, there is a ratio, with very special properties, that many artists through the centuries have favoured, sometimes without being aware of it. This ratio is defined in this way: The shorter distance divided by the longer distance is equal to the longer distance divided by the whole distance.
A related task is to create a rectangle with the most pleasing proportions.
The solution, perhaps too obvious, is to make all sides equal, in other words to create a square. The ratio of any two adjacent sides is 1 : 1.
The third task is more complex and interesting: create a rectangle so that dividing it down the centre creates two rectangles of the same proportions (but rotated 90 degrees) as the original.
The solution to this task turns out to be the basis for our standard paper sizes: A3, A4, A5, A6 and so on, and the ratio is √2 : 1 (approximately 1.414 : 1).
The fourth and final task is to create a rectangle so that removing a square from one end creates a smaller rectangle of same proportion as the original.
E.g. Joshua Reynolds’ portrait of James, the seventh Earl of Lauderdale

James, 7th Earl of Lauderdale
Coll. Art Gallery of NSW
The area below the ledge on which the crown sits is a square. The area above the ledge is a rectangle with the same proportion as the whole painting.
As it turns out, the last solution to this problem is essentially the same as the last solution to our first problem. And that ratio is approximately 1.618 : 1. Its exact value (which can be proven with fairly simple algebra 1 ) is √5-1 : 2. It has its own special name: the golden ratio. It even has its own mathematical symbol: Φ (the Greek letter phi) 2 .
Most artists acknowledge the importance of relationships, and specifically proportion (even if not mathematically calculated proportion), as important components of an artwork, specifically of its composition. But for some artists, proportion is everything; anything else is a distraction. One such artist is Piet Mondrian. In Mondrian’s mature style (typically interlocking rectangles in white, red, yellow and blue, with thick, black lines), every painting is a representation (or “distillation”) of the whole world. Now Mondrian didn’t just suddenly arrive at this way of working. If you look at his earlier work, through the second decade of the twentieth century, you will see that he was gradually moving from the individual to the general, searching for the “essence” of things. This is known in art as abstraction or, more generally, reductionism. Reductionism means that chaos is transformed into order and complexity is transformed into simplicity.
As we shall see a little later, some artists prefer to travel in the opposite direction, from order to chaos.
What is mathematics?
If you were to ask a number of mathematicians “What is mathematics?”, you would probably get many answers. Most, however, would boil down to one of two basic views. One says that mathematical “objects” exist independently of our knowledge of them. The other view says that there is no such thing as a mathematical “object” and that mathematics is simply the manipulation of symbols according to systems of rules, systems invented by mathematicians. The first view is called “Platonism” (after Plato, who believed that there was a perfect world of pure form behind the reality we experience in everyday life) and the second is called “Formalism” (because it sees mathematics as a formal system). Platonists will often say that they are discovering mathematical theorems, whereas formalists will often say they are just playing with symbols.
There are parallels with art already. Some artists (e.g. Piet Mondrian or Kasimir Malevich) see the images they create as manifestations of some underlying truths, or principles, and will therefore attempt to distil more and more, until their works describe as closely as possible those essential truths. Other artists (such as Andy Warhol) treat the language of art as the subject of art, so their works become a series of experiments in how symbols create “meaning” 3 .
Stepping out of the system
The essence of mathematics (and science) is asking, not what? or how? or how many? (at least not only those questions) but why?
To ask why is to step back from (or out of) a system – to see the system behind the system, or, in other words, the “meta-system”. But, of course, if there is a meta-system, there must be a meta-meta-system, and so on. (Clearly the significance of this “stepping outside of systems” would be different for a Platonist and a Formalist.)
This also raises an interesting philosophical question (almost a theological one): is there a “Grand System” behind all systems, or is it “turtles all the way down” 4 ?

La condition humaine, 1933
Coll. NGA, Washington, DC
Some interesting results occur when we mix levels, in art as well as mathematics. For example, consider this painting, by the Belgian Surrealist, Rene Magritte:
What is the semiotic “joke” operating here (that is, a joke about symbols and meaning)? It is that there is no difference between representation and “reality”, because the paint describing the image on the canvas (on the easel in the picture) is no less real than the paint describing the buildings or the grass.

Print Gallery 1956
Coll. NGA, Washington, DC
Now consider this work by the Dutch artist, M.C. Escher:
If you look carefully, you will see that the city contains the gallery, which contains the picture, which “contains” the city, which contains the gallery, which contains the picture, and so on.
These are indeed paradoxes and we know that they are strange. Yet, in everyday life, we switch from one level or meaning to another all the time. For example, earlier, I wrote: “In this essay … I will attempt to … examine the principles and philosophies of these two disciplines.” In other words, in my essay, I referred to the essay itself!
This “illegal” switching between levels is normally not a problem, but in mathematics and logic, fuzziness such as this can lead to paradoxes. These can be infuriating or fascinating, depending on your point of view. Let’s have a look at a few paradoxes of logic. Take some time to digest their absurd implications.
The first (and the simplest) uses self-reference:
This statement is false.
The second uses circular reference:
The following statement is false.
The previous statement is true.
The third uses infinitely cumulative reference:
At least one of the following statements is false.
At least one of the following statements is false.
At least one of the following statements is false. … etc.
Paradoxes and set theory
One field of mathematics, which many mathematicians believe is the basis of mathematics itself, is set theory. In one sense, set theory is very simple (which is why it has been taught in primary/elementary schools); yet in another sense it is very profound.
A set is simply a collection of “things”. Here are some examples of sets:
A: The set of all the people in the same room as you.
B: The set of all the people who have ever lived who are not in the same room as you.
C: The set consisting of Cate Blanchett, the territory of Australia, the number 3 and Bach’s Air on G.
D: The set consisting of everything in the universe other than Cate Blanchett, the territory of Australia, the number 3 and Bach’s Air on G. (including other sets!). This is described as “not C”, and written “~C”.
E: The set consisting of Set A combined with Set D. This is described as “The union of A and D”, and written “A ∪ D”.
F: The set consisting of those members of Set A that also belong to Set D. This is described as the intersection of A and D, and written “A ∩ D”
Note that we do not need be able to count the members, the members do not have to be physical objects and the members do not have to have anything in common other than the fact that we have grouped them into a set. The only requirement is that the members (or elements) be well-defined.
Here is another curious paradox, based on set theory: Define a set: the set of all sets. We shall call this “U” (for “Universal”). If U is the set of all sets, then clearly it must be a member of itself. Now define another set: the set of all sets that do not contain themselves. We shall call this “X”. The question is this: is U a member of the set X? If the answer were yes, then this would mean that U is not a member of X. If the answer were no, then this would mean that U is a member of X! The source of the paradox is that we have used words to only seemingly create a well-defined set (X); it seems to be well-defined but it isn’t.
Escher’s Print Gallery is basically an image about a set-theory paradox.
Crises
The history and evolution of mathematics, like that of art, has been marked by a series of crises: times when previously accepted principles have been overturned.
The earliest use of “mathematics” was counting objects (probably possessions). So numbers were: “1, 2, 3, 4, …” and so on. Theoretically there was no largest number, but in practice it was determined by the likelihood that you would have that many things to count. Then, fractions were introduced. This was not exactly a crisis, but definitely a conceptual jump. For the first time humans could divide pies fairly between a group of people.
Zero
The first real crisis was zero. Without zero, mathematics as we know it (i.e. the place-value system that represents ten as 10 and one hundred as 100, rather than X and C respectively) would be impossible.
So why was zero a crisis? It was partly confusion (“How can ‘nothing’ be a number?”) and partly fear – of the great unknown, the “abyss”.

Void Field 1980s
Coll. Art Gallery of NSW
Here is an example of an artwork that addresses the issue of the “zero-abyss”:
Kapoor’s Void field consists of four large blocks of Cumbrian stone, each one with a thirty centimetre hole in the top. The inside of each block is so dark and unreflective that it is impossible to know just by looking how deep the hole is. It becomes in effect an infinite nothing.
Negative numbers
Negative numbers made financial transactions (with their credits and debits) possible, amongst other things. Yet they too caused a crisis when they were first introduced. Why? It is because they stretched the basic concept of “number”. Number originally meant a one-to-one correspondence between two sets: a set of objects to be counted and a set of abstract “units”. So, how can you have minus 5 sheep?

Head of a Woman. c1917-20 (after a work of 1916)
Coll. MoMA, NY
Look at this sculpture by the Russian Constructivist, Naum Gabo.
This effect is often called “negative space”; however it is more accurately described as negative curvature (concave instead of convex).
Normally in sculpture, there is a balance between positive and negative curvature (for example, the work of Henry Moore), but in this sculpture (and many others by the Russian Constructivists), negative curvature dominates, giving the impression that space has been turned inside out.
Irrational numbers
Imagine a square one unit by one unit. Pythagoras proved that the length in units of the diagonal is a number which, when squared, equals two (i.e. √2).
Why was this a crisis? Mathematicians once believed that every number could be expressed as the ratio of two whole numbers. So, for example 3 = 3/1 and 3.127 = 3127/1000. This is the basis of measurement: you measure, say, length by using a stick which has been marked with divisions and subdivisions. But it can be proved, without too much difficulty 5 , that there is no number p/q (where p and q are whole numbers) that, when squared, gives 2. The consequence is that you could have a distance – or any quantity – that could never be measured exactly, because it cannot be expressed as a fraction. Such numbers are called “irrational”, because they cannot be expressed as a ratio.
Non-Euclidean geometry
Euclid’s fifth axiom 6 of geometry is illustrated in the diagram below. It states that if you have a line (L) and a point not on that line (P), you can draw one and only one line that passes through this point that is parallel to the original line. (This is of course assuming that everything is on a single plane.)
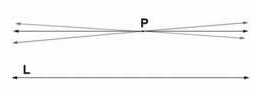
Non-Euclidean geometry is a system built on not accepting this axiom as true. In normal (Euclidean) geometry, the sum of the three angles in any triangle is always 180 degrees. In non-Euclidean geometry, however, the sum could be greater than 180 degrees, or less than 180 degrees. Although it contravenes “commonsense”, it is perfectly consistent as a system, meaning that it will never lead to any internal contradictions.
The reason why Non-Euclidean geometry was a crisis is harder to explain than negative and irrational numbers, but Euclid’s five axioms had been the basis of geometry for centuries. Also, the system of “proofs resting on proofs, resting on proofs, and so on, resting on the axioms”, had been the model for how the whole of mathematics worked. Non-Euclidean geometry challenged, or rejected, the absoluteness of the axioms.
Infinitesimals
Infinitesimals are quantities greater than zero but smaller than any other positive number. This is the basis of calculus, which was used for centuries because it produced correct answers, although many mathematicians still regarded it as illogical. This is the opposite of a paradox: It “shouldn’t” work, but it does!

Suprematist Composition: White on White 1918
Coll. MoMA, NY
Kasimir Malevich’s Suprematist Composition: White on White is like an “infinitesimal” painting: it is as hard to see as you could possibly get and yet still be called a painting.
Imaginary (and complex) numbers
When you square a positive number, you get a positive number (e.g. 4 x 4 = 16); when you square a negative number, you also get a positive number (e.g. -4 x -4 = 16), because the two negatives “cancel each other out”. So, if the square of any number is always positive, how can a negative number have a square root? With “real” numbers, it can’t. But what if we imagine that we can; what if we say that the square root of -1 is “i” (for “imaginary”)? If we do, then i2 = -1 and √-4 = 2i.
Describing numbers as either “imaginary” or “real” seems to imply that there is some sort of hierarchy or value-judgement. Mathematicians now admit that the names are illogical and arbitrary, but the names have stuck, and they are convenient 7 . In fact, real and imaginary numbers can also be combined to form “complex numbers” (e.g. 3i+7).
Infinite numbers
Mathematicians had long accepted the concept of infinity (there is no such thing as “the highest possible number”) and, more recently, infinitesimals. However, the next crisis was the concept that there was a variety of infinite numbers.
You might be asking yourself: “How can one infinity be bigger than another?”
Consider this grid, of rational numbers, or fractions:

You will see that the numerators (the top numbers in the fractions) increase by one each time we step across the grid, and the denominators (the bottom numbers) increase by one each time we step down. So, if the grid were extended forever across and down, every rational number would be have to be listed at least once. If you were a postman and you had to deliver mail to every fraction in the grid, which path would you take? It would be no good doing the top row first, because you would never get to the next row. Likewise for the left-hand column. The solution is to follow a path like the one in blue, below:

By following this path shown, any specified rational number would be reached – eventually, that is, after a definite number of steps. This means that the set of rational numbers can be “counted”, because for any member there is a corresponding member of the set of whole numbers. This one-to-one correspondence is sometimes called “mapping”.
The infinity that can be mapped to the set of whole numbers is called ℵ0 (pronounced “Aleph null”). It was called this by the pioneer of infinite number theory, Georg Cantor.
Hopefully you are wondering, can we break through the barrier of ℵ0 to a larger infinite number?
Let’s compile a list of unique real numbers between 0 and 1, expressed as decimals. These may be rational or irrational. Here is the beginning of one such list, showing the first nine decimal places for each number:
r(1) = . 1 4 1 5 9 2 0 5 3
r(2) = . 3 3 3 3 3 3 3 3 3
r(3) = . 7 1 8 2 8 1 8 2 8
r(4) = . 4 1 4 2 1 3 5 6 2
r(5) = . 5 0 0 0 0 0 0 0 0
r(6) = . 2 4 4 9 1 9 3 1 0
r(7) = . 0 5 8 8 2 4 1 9 7
r(8) = . 9 8 7 6 5 4 3 2 1
r(9) = . 0 0 1 0 2 5 5 2 9
Because they are in an infinite series, there are ℵ0 of them. However, we can create a new number by using the first digit of r(1), the second digit of r(2), the third digit of r(3), and so on, but adding one each time (unless the digit is 9, in which case it becomes 0). So, in this example, following the bold digits down the diagonal, we have .138209129… Then, adding one, we get .249310230… This could not be equal to any of the existing numbers in our series because it differs in at least one decimal place from each of them. This shows that there can never be a one-to-one correspondence between the two sets. Therefore there are more real numbers between zero and one than all whole numbers!
So, there must exist a larger, or “higher order”, of infinite number, which is called ℵ1 (“aleph one”). In fact there are even larger infinite numbers than this.
The final crisis (and by far the deepest) arose indirectly out of infinite number theory.
Incompleteness theorem
We have established that the number of whole numbers is ℵ0 and the number of real numbers is ℵ1. Some mathematicians wondered, is there an infinite number between ℵ0 and ℵ1? In 1878, Cantor stated that his “hunch” (or hypothesis) was no. This is known as the Continuum Hypothesis. For sixty years mathematicians strove to prove or disprove this. Finally, in 1938, the German mathematician Kurt Gödel (pronounced “girdle”) proved that the Continuum Hypothesis (CH) is consistent with set theory, but unprovable (that is, it will never lead to a contradiction). But then, the same is true for the opposite of the Continuum Hypothesis (i.e. that there is at least one infinite number between ℵ0 andℵ1).
So, which should we accept? The answer, believe it or not, is… either! However it is simpler to assume that CH is true. This is the principle known as “Occam’s Razor” (“If there are two opposing theories and neither can be proved or disproved, accept the simpler”).
Gödel was able to generalise his proof to assert: “There are statements about number theory which are consistent with, but unprovable with, the system of number theory.” 8
This is related to Heisenberg’s famous uncertainty principle in physics 9 . The uncertainty principle and chaos theory are related to the quantum nature of the universe. But surely, we might think, the abstract field of mathematics is immune from that! Apparently not.
Gödel drove an extra wedge between Platonism and Formalism: The Platonists responded to his theorem by claiming: “The formal system is too weak.” The Formalists responded by claiming: “The Platonistic view is meaningless because axioms are arbitrary.”
Crises in art
It is much harder to say what the first crisis in art was. Compared to mathematics, the purpose, and hence definition, of art is much less clear, especially in prehistory. However, three crises with particular relevance to art, as we understand it now, are relativity, object-autonomy and uncertainty.
Relativity
To believe in relativity is to reject the notion that it is possible to make a true and objective representation of a subject.

Madonna and Child with Saints Jerome, John the Baptist, Bernardino and Bartholomew c.1450-81
Coll. Art Gallery of NSW
The Siennese artist, Sano di Pietro, represents the Virgin Mary, the infant Jesus, various saints and angels against a gold-leaf background as though they are all in heaven. The saint to the left of Mary is the adult John the Baptist who, according to the Bible, was born around the same time as Jesus.
By placing his figures within an architectural setting and employing the relatively new technique of linear perspective, the Florentine Renaissance artist, Raphael, defines his position in space, relative to the subject. It is as though he were there, at the moment that Mary and Jesus were enthroned. Ironically, the artist has used a technique that says “I was an eye-witness to this event” to construct a scene from his imagination.

The prodigal son 1885-87
Coll. Art Gallery of NSW
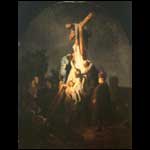
The deposition 1633
Coll. Alte Pinakothek
However, relativity in art is not restricted to just space and time. Consider the following two artworks:
Both artists (Rembrandt and Rodin) describe their personal, emotional response to the subject.

Grainstack, sun in the mist 1891
Coll. Minneapolis Inst. of Arts
The Impressionist artist, Claude Monet, describes the sensations he experienced at a particular time, on a particular day, looking at these haystacks. The effects of light and atmosphere have affected his perception of the subject.
To summarise, relativity in art presents the world as it seems rather than as it “is”.
Object-autonomy
Once artists learnt to use linear perspective to describe their subject as it appeared to them, paintings became windows on virtual worlds, complete with “window” frames. In contrast, the further one goes back in the history of art, generally speaking, the more the image is identified with the subject, in an almost magical way (e.g. Egyptian tomb painting).

Pastoral landscape 1636-37
Coll. Art Gallery of NSW
Consider this painting, by the French seventeenth-century artist, Claude Lorrain:
The painting creates the illusion that we are looking into an imaginary (and idealised) world. The technique needs to be very fine, because, if we could see brushstrokes it would burst the “illusion-bubble”; it would be like seeing a microphone boom in a movie.
Paradoxically, the art movement that many believe heralded modern art – Impressionism – was involved in the crisis of relativity and a crisis that challenged this “image-as-illusion” convention.
Look at the painting by Monet, Grainstack, sun in the mist, again. Even at this low resolution (or at a distance of, say, five metres from the original), the brushstrokes are obvious. Many people say that Impressionist paintings need to be seen from far away, because then you can see “what it’s supposed to look like”. But this is to misunderstand the Impressionists’ intention. Impressionist artists used large, thick brushstrokes (sometimes marks made with a palette knife) and broken, high-intensity colour very deliberately. What would be the point if the viewer were supposed to view their paintings from so far away that they resembled any other nineteenth century paintings?
One contemporary viewer of Impressionist paintings was the Russian Vasily Kandinsky. Here he recalls his first encounter with a Monet painting of a haystack, probably not unlike the one illustrated above.
“The catalogue explained to me that it was a haystack. I could not recognise it. I felt embarrassed at this lack of recognition. I also felt that the painter had no right to paint so indistinctly. I had a dull feeling that the object was missing. … The thing, however, that was completely clear was the unexpected power of the palette, until now unknown to me, which surpassed all my dreams.” 10
This “power of the palette” was the autonomy of the painted surface. It was no longer an image that merely pretended to be something else – an illusion – it was an object in its own right.

Study for painting with the white border 1913
Coll. Art Gallery of NSW
And here is a work by Kandinsky, coincidentally painted the same year that he wrote about his earlier encounter:
Uncertainty
This is the closest parallel to crises in mathematics and physics: Gödel’s Incompleteness Theorem and Heisenberg’s Uncertainty Principle, respectively. We will approach it by considering the question: where does an artist’s imagery come from?
Let’s begin with three works by the French avant-garde artist, Marcel Duchamp.

Man seated by a window (1907)
Coll. MoMA, NY
For all its acknowledgment of the achievements of Post-Impressionism (for example, the distorted colours of Van Gogh or Gauguin), this painting is still essentially a case of finding an enduring, two-dimensional “equivalent” of a fleeting visual experience (what is sometimes referred to as “look and put”).

Nude descending a staircase (No. 2) 1912
Coll. Philadelphia Museum of Art
Approximately five years later and Duchamp is starting to let the image have a life of its own (thanks to the lessons of Cubism).

Bicycle Wheel 1913
Coll. MoMA, NY
One year later and suddenly Duchamp turns his back on the assumption that an art image must be created directly by its artist. This particular work has been created simply by inserting an upturned front wheel of a bicycle into a stool, although other works (referred to by the artist as “readymades”) are just single objects that he declared to be artworks. As long as the artist chooses it, that is enough.

Study for painting with the white border 1913
Coll. Art Gallery of NSW
Kandinsky approaches the same crisis from a different angle:
Unlike Duchamp, Kandinsky retains the tactility of the creative process, but rejects the attachment to any specific motif in front of him. This is an example of the mind “free-wheeling”.

Number 1, 1950 (Lavender Mist) 1950
Coll. NGA, Washington, DC

Almost forty years later, in the USA, an artist named Jackson Pollock pushes this idea even further:
Pollock’s paintings are as much about the laws of physics (for example, acceleration due to gravity and the dynamics of liquids), and human kinesiology, as they are about the artist’s “inner emotional life” – possibly more so.
However, for all their brave attempts to break free of the confining assumptions about how artists create artworks, Duchamp, Kandinsky and Pollock all assumed that there were basically two elements: the artist and the artwork (then later, the audience).

Anthropometry: Princess Helena 1960
Coll. MoMA, NY

Performance of Anthropometry
But what if the artist relinquishes even this? Here we see the creation of an artwork by the French artist Yves Klein, and then the artwork itself:
How can we say, with confidence, that Yves Klein is the artist of this work? Perhaps he is more of a director, or a conductor; and here lies both danger and liberation.

Here is an image that will probably look familiar to many people – the Mandelbrot pattern. It is a pattern with, literally, infinite complexity, produced entirely by an amazingly simple mathematical formula:
un+1 = un2 + c
u0 = 0
{un} bounded if and only if c ∈ M
This could be the greatest surprise in mathematics (for artists at least): that processes which are totally algorithmic and mechanical, processes that should be totally deterministic and predictable, can in fact be wild and unpredictable.

So, perhaps we should we leave art-making to algorithms, performed by computers? For example, Apple’s iTunes Visualiser (which began life as a standalone program called G-Force).
The skill and sensitivity are not in the creation of any particular image or image sequence (after all, the computer is not skilful or sensitive, just extremely fast at carrying out instructions). They are in the creation of the code that will respond to volume, pitch and rhythm, feed back on itself to create unexpected and unpredictable (i.e. chaotic) patterns and yet (mostly) retain a sense of coherence.

Ariokasi 2001
However, an algorithmic creative process need not be devoid of human intervention and involvement. For example, George Barker, a Sydney-based printmaker, programs a computer to create images for him. The art is in the programming.
Paradoxically perhaps, far from being a way of “taming” art, mathematics can be a way to liberate art and the artist.
Footnotes
[––– x –––][–––– 1 ––––]
[––––––––– x+1 ––––––––]
x/1 = 1/(x+1)
1 = 1/x(x+1) : dividing both sides by x
1 = x(x+1) : getting reciprocal of both sides
= x2+x
x2+x = 1 : swapping sides
x2+x-1 = 0 : subtracting 1 from both sides
x = (-1±√(12-(-4)))/2 : solving quadratic equation
= (-√5 – 1)/2 or (√5 – 1)/2
But x can’t be negative, so the solution has to be…
x = (√5 – 1)/2
2.
Φ can be defined in a number of ways:
- x such that 1/x = x/(x+1)
- Proportion of rectangle where removing square produces an identical, but smaller, rectangle
- (√5 -1)/2
- limn→∞(fibn+1/fibn)
- 2 cos(π/5)
- Chord of a regular pentagon with unit sides
- 1+(1/(1+(1/(1+(1/(1+(1/(1+…
3.
As a quick demonstration of mathematical formalism, consider the following game, involving the creation of different sequences of the symbols “p”, “e” and “.”:
There are four basic rules:
- Only some sequences are allowed (or valid).
- There is one given, valid sequence: .p.e..
- This is the rule for generating new valid sequences: Let’s use x, y & z to represent 3 strings of dots.
[Note: x, y & z are not part of the system; they only stand in for strings of dots]
If xpyez is a valid sequence, then xpy.ez. is also a valid sequence. - The object of the game is to generate more valid sequences – as many as you can.
Try it. After a while, you will probably notice a pattern to the sequences that are generated: valid sequences seem to be “about” simple addition.
E.g. “.p..e…” is like “1+2=3”.
This is called isomorphism:
“p” corresponds to “plus”; “e” corresponds to “equals”; “.” corresponds to “one”, “..” corresponds to “two”; “…” corresponds to “three”, etc.
So, “.p..e…” would translate as “one plus two equals three” (which makes “sense” to us).
But is this really any more “valid” an isomorphism than “p” corresponding to “bone”, “e” corresponding to “dog” and “.” corresponding to “happy”? This would make “.p..e…” translate as “happy bone happy happy dog happy happy happy” (which probably would make perfect sense to a dog!).
4.
A story is told of a scientist who had just finished giving a lecture on evolution when an elderly woman came forward to inform him that she believed the world rested on the back of a giant turtle. The scientist asked the obvious question: “On what does the turtle stand?” She smiled and said, “You’re clever, but not clever enough to catch me; it’s turtles all the way down.”
5.
Proof that √2 is irrational:
Temporarily assume that √2 is rational: √2 = p/q (where p & q are whole numbers with no common factors)
Square both sides: 2 = p2/q2
If p and q have no common factors, then p/q cannot be simplified (or “cancelled out”). Similarly for p2/q2.
But if p2/q2 cannot be simplified in general, then it cannot be simplified in particular down to the number 2, which contradicts the previous equation (2 = p2/q2).
Therefore our original assumption must have been false.
Therefore √2 must be irrational.
6.
An axiom is something that does not need to be proved, because it is “self-evident”.
7.
Here’s an interesting question: Why is √-1 allowed but 1/0 is not?
| For all n: 0 x n = 0 | So… 0 x (1/0) = 0 | §1 |
| For all n: n x (1/n) = 1 | So… 0 x (1/0) = 1 | §2 |
| §1 and §2 | 0=1 | §3 |
| Add 1 to both sides of §3 | 1=2 | §4 |
| §3 and §4 | 0=2 | §5 |
| … and so on | ||
In other words, the whole number system would collapse to 0.
8.
Paraphrased for simplicity.
9.
At any given moment the position or the momentum of a particular subatomic particle can be measured, but never both.

Quite informative data, but can you please provide all reference regarding this topics? Also I am curious to know different styles of art and logic of creating modern art, representation of concept using symbolism. All reference regarding these things will be quite helpful.